4.4多重循环
【例4.21】
对于给定的自然数n,输出1-n之间全部质数。
- 分析: 要输出1~n之间的全部质数,就要判断每一个数是否是质数。而判断质数的问题,我们在之前已经解决了。那么本题就只要重复进行进行n次质数的判断。
程序如下:
#include<iostream>
using namespace std;
int main() {
int n, m, i;
cin >> n;
for (m = 2; m <= n; m++) {
i = 2;
while (m % i != 0 && i <= m - 1) {
i++;
}
if (i > m - 1) {
cout << m << " ";
}
}
return 0;
}
- 说明: 循环体内可以出现任何语句,当循环体中又出现循环时就构成了多重循环,本题中在for循环的循环体中出现了while循环,本节我们将学习应用多重循环解决实际问题的方法。
- 带着这些问题,本节我们将学习C++语言的whie循环语句。
4.4.1多重循环的使用方法
- for循环、while循环和do-while循环的循环体中都可以出现任何一中循环语句。下表都是多重循环的语句形式。

【例4.22】
写出下列程序的运行结果。
程序如下:
#include<iostream>
using namespace std;
int main() {
int i, j;
for (i = 1; i <= 5; i++) {
j = 5;
while (i <= j) {
cout << i * 10 + j << " ";
j--;
}
cout << endl;
}
return 0;
}
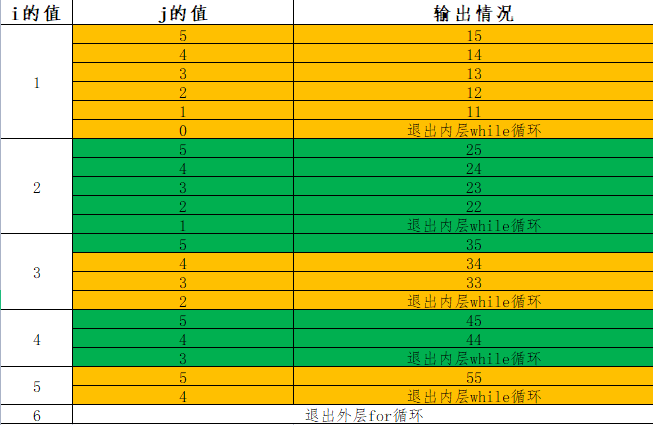
- 说明: 对于多重循环而言,外层循环执行一次,内层循环执行若干次,直到内层循环的表达式为假,外层循环才执行下一次操作。
- 根据上述说明,程序第5行for循环中的i每取得一个值,第7行的while循环就要执行i<=j的所有情况。
- 我们可以用下表来模拟程序的执行过程:
【例4.23】
百钱买百鸡问题。鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱一,百钱买百鸡,问鸡翁、鸡母、鸡雏各有几何?
- 方法一: 在数学中解决这个问题,我们通常会列一个方程组,设鸡翁x,鸡母y,鸡雏z,则有
- x+y+z=100
- 5*x+3*y+z/3=100
- 同时满足上述方程的x,y,z的解就是所求。
- 根据这个思想,问题就转化为了求方程组的解,我们列举x,y,z的所有肯能,然后判断这些可能是否能够时得方程组成立,能使方程组成立的就是真正的解。
- 在进一步分析可得,x的取值范围为:0~100/5,x的取值范围为:0~100/3,z的取值范围为0~100
程序如下:
#include<iostream>
using namespace std;
int main() {
int x, y, z;
for (x = 0; x <= 100; x++) {
for (y = 0; y <= 100; y++) {
for (z = 0; z <= 100; z++) {
if (x + y + z == 100 && 5 * x + 3 * y + z / 3 == 100) {
cout << x << " " << y << " " << z << endl;
}
}
}
}
return 0;
}
- 思考: 这里用了三层循环来解决问题,当x取得一个数值时,y的循环体需要遍历y的所有取值,对于y的每一个取值,z的循环体也要遍历z的所有取值,对于z的每一个取值,if语句都要执行一次 ,因此不难算出,在程序的执行过程中,作为内层循环体的if语句需要被执行的次数大概为:。
- (100/5)*(100/3)*100
- 这个次数大概为6万次,那我们有没有其他方法能够减少程序执行的次数,提高效率呢?
- 方法二: 鸡翁,鸡母,鸡雏共100只,一旦确定了鸡翁的数量x和鸡母的数量y,鸡雏的数量也就确定了:(100-x-y)
- 因此我们可以尝试写出两层循环的程序
程序如下:
#include<iostream>
using namespace std;
int main() {
int x, y, z;
for (x = 0; x <= 100/5; x++) {
for (y = 0; y <= 100/3; y++) {
z = 100 - x - y;
if (x + y + z == 100 && 5 * x + 3 * y + z/3 == 100) {
cout << x << " " << y << " " << z << endl;
}
}
}
return 0;
}
- 说明: 对于与本题类似的求解不定方程问题,都可以用循环来解,为了提高效率,可以在程序中进行优化,减少循环体的执行次数。
练习题
- (1) 输入一个正整数n,输出高度为n的由*组成的等腰三角形,如下图所示:

- (2) 输入一个正整数n,输出乘法口诀表的前n行,如下所示;
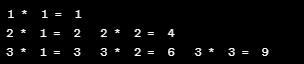
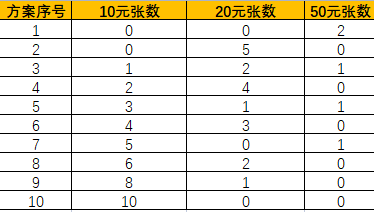
- (3) 将任意给定的整百元钞票兑换成10元、20元、50元小钞票形式,输出兑换方案的总数。
- 输入样例:
- 100
- 输出样例:
- 10
- 方案举例:
- (4) 数根是这样定义的:对于一个正整数n,将它的各个数位上的数相加得到一个新数,如果这个数是一位数,我们就称之为n的数根,否则重复处理直到它成为一个一位数。
- 例如,n=34,3+4=7,7是一个一位数,所以7是34的数根。
- 再比如,n=345,3+4+5=12,1+2=3,3是一个一位数,所以3是345的数根。
- 对于任意输入的n,编程计算它的数根。
- 输入样例:
- 345
- 输出样例:
- 3