3.3if嵌套语句

3.3 if嵌套语句

【例3.15】 输入年份year，输出该年是否为闰年。

分析： 在例3.10中用逻辑表达式表示闰年的条件，对于年份能否被400整除或者能被4整除但不能被100整除的闰年条件，也可以用下图来表示。

程序如下：

                            #include<iostream>
                            using namespace std;
                            int main() {
                                int year;
                                cin>>year;
                                if (year % 400 == 0) {
                                  cout<<year<<"是闰年"<<endl;
                                } else {
                                  if (year % 4 == 0) {
                                    if (year % 100 == 0) {
                                      cout<<year<<"是闰年"<<endl;
                                    } else {
                                      cout<<year<<"不是闰年"<<endl;
                                    }
                                  } else {
                                    cout<<year<<"不是闰年"<<endl;
                                  }
                                }
                                return 0;
                          }

说明： 对应上图判断year是否是闰年的分支求解过程，在程序的表达过程中，我们自然而然的用到了if的嵌套，那么，使用if的嵌套语句我们应该注意什么？如何正确应用嵌套if去解决问题？为了回答这些问题，我们将详细学习嵌套if的使用。

3.3.1 if嵌套语句

if嵌套语句是指在if……else……的某个分支中还存在if……else……语句。
在例3.15的程序中，用了3层if嵌套语句。在用if嵌套语句表达问题时，最重要的是先把事情的分支逻辑梳理清除，如上图所示，把判断闰年的分支逻辑梳理清除，接着用if表达分支逻辑关系就很简单了。
在使用if嵌套语句时，需要注意if与else的配对关系，else总是和在它前面的离他最近的且未配对的if配对。

【例3.16】随机输入一个年份year，判定并输出该年是否为闰年。

分析：分析下面两个程序的区别。

程序1如下：

                            #include<iostream>
                            using namespace std;
                            int main() {
                                int n;
                                cin>>n;
                                if (n % 3 == 0)
                                  if (n % 5 == 0)
                                    cout<<n<<"是15的倍数"<<endl;
                                  else
                                    cout<<n<<"是3的倍数，但不是5的倍数"<<endl;
                                cout<<"结束"<<endl;
                                return 0;
                            }

说明： 程序中的else要与它前面的最近的且未配对的if配对，因此与第二个if配对，语句3只针对被3整除的数，判定输出“是15的倍数”还是“是3的倍数但不是5的倍数”。

程序2如下：

                            #include<iostream>
                            using namespace std;
                            int main() {
                                int n;
                                cin>>n;
                                if (n % 3 == 0) {
                                  if (n % 5 == 0)
                                    cout<<n<<"是15的倍数"<<endl;
                                }
                                else cout<<n<<"不是3的倍数"<<endl;
                                cout<<"结束"<<endl;
                                return 0;
                            }

说明： 语句中的else与第一个if配对，两个程序的差别虽然仅仅在于一对“{}”，但逻辑关系完全不同，一些数据的运行结果也不同。为了清楚的表达if嵌套语句，我们在写程序的时候会采取缩进的方式，让同一层次的if与else进行对齐。

【例3.11】 输入三角形的三条边a,b,c的值，判断能否构成三角形，如果能，请求出三角形的面积？

分析：根据数学定理，构成三角形的三条边满足任意两边之和大于第三边的条件，逻辑表达式如下:
a+b>c&&b+c>a&&a+c>b
当表达式a+b>c&&b+c>a&&a+c>b的值为真时，a,b,c能够构成三角形，否则不构成三角形，也可以说成只要有某两边之和小于等于第三边时a,b,c就不能构成三角形，其逻辑表达式如下：
a+b<=c||b+c<=a||a+c<=b

两边之和大于第三边的程序如下：

                            #include<iostream>
                            #include<cmath>
                            using namespace std;
                            int main(){
                                float a,b,c;
                                float p;
                                float s;
                                cin>>a>>b>>c;
                                if(a+b>c&&a+c>b&&b+c>a){
                                    p=(a+b+c)/2;
                                    s=sqrt(p*(p-a)*(p-b)*(p-c));
                                    cout<<"三角形的面积为："<<s<<endl;
                                }else{
                                    cout<<"不能构成三角形"<<endl;
                                }
                                return 0;
                            }

任意两边之和小于等于第三边不构成三角形，否则构成三角形的程序如下：

                            #include<iostream>
                            #include<cmath>
                            using namespace std;
                            int main(){
                                float a,b,c;
                                float p;
                                float s;
                                cin>>a>>b>>c;
                                if(a+b<=c||a+c<=b||b+c<=a){
                                    cout<<"不能构成三角形"<<endl;
                                }else{
                                    p=(a+b+c)/2;
                                    s=sqrt(p*(p-a)*(p-b)*(p-c));
                                    cout<<"三角形的面积为："<<s<<endl;
                                }
                                return 0;
                            }

思考： 两个程序分别使用逻辑与和逻辑或来解决问题的，那么，逻辑与和逻辑或能不能相互转化呢

3.3.2if嵌套语句的应用

【例3.17】 输入三个数，输出其中最大的数。

方法1： 设maxn用于存放三个数中的最大数，输入的三个数存放子a，b，c中，那么如果a比b和c大，则最大数是a，如果b比a和c大，那么最大数是b，否则最大数是c。

程序如下：

                            #include<iostream>
                            using namespace std;
                            int main() {
                                float a, b, c, maxn;
                                cin>>a>>b>>c;
                                if (a > b && a > c)
                                  maxn = a;
                                else if (b > a && b > c)
                                  maxn = b;
                                else
                                  maxn = c;
                                cout<<"最大数为："<<maxn<<endl;
                                return 0;
                          }

方法2： 设maxn用于存放三个数中的最大数，输入的三个数存放子a，b，c中，初始化时maxn=a，即先假设a是三个数中的最大值，接下来用b和maxn比较，如果b>maxn，那么此时b是a，b两个数中的最大值，即maxn=b，否则maxn还是等于a，（此时maxn中存放了a，b两个数中的最大值），然后用c和maxn再比价，如果c>maxn，说明c比a，b中的最大值要大 c就应该是三个数中的最大值，即maxn=c，否则maxn还是等于a，b中的最大值。

程序如下：

                            #include<iostream>
                            using namespace std;
                            int main() {
                                float a, b, c, maxn;
                                cin>>a>>b>>c;
                                maxn = a;
                                if (b > maxn) maxn = b;
                                if (c > maxn) maxn = c;
                                cout<<"最大数为："<<maxn<<endl;
                                return 0;
                          }

思考？： 假如我们要找10个数中的最大数，应该用哪种方法比较好，为什么？

【例3.18】 输入三个数，按照从大到小的顺序输出。

方法1： 输入的三个数存放在a、b、c中，那么存在下面几种情况。。

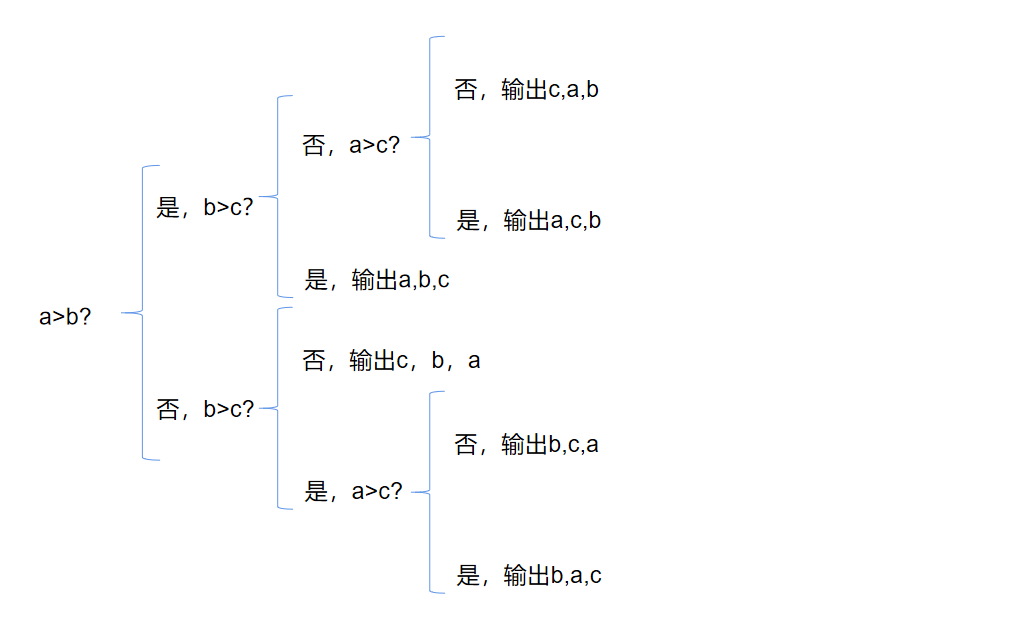
程序如下：

                            #include<iostream>
                            using namespace std;
                            int main() {
                                float a, b, c;
                                cin>>a>>b>>c;
                                if (a > b) { //确定a在b的前面，接着确认c的位置
                                  if (b > c) //确定b在c的前面
                                    cout<<a<<","<<b<<","<<c;
                                  else { //确定c也在b的前面，接着确认a和c谁在前面
                                    if (a > c)
                                      cout<<a<<","<<c<<","<<b;
                                    else
                                      cout<<c<<","<<a<<","<<b;
                                  }
                                } else { //确定b在a的前面，接着确认c的位置
                                  if (b > c) { //确定b也在c的前面，接着确认a和c谁在前面
                                    if (a > c)
                                      cout<<b<<","<<a<<","<<c;
                                    else
                                      cout<<b<<","<<c<<","<<a;
                                  } else
                                    cout<<c<<","<<b<<","<<a;
                                }
                                return 0;
                            }

方法2： 输入的三个数存放子a，b，c中，假设我们最终让a存放三个数中最大的数，怎么实现呢？让a和b比较，如果a<b，那么将a和b的值进行交换，保证a>=b; 接着让a和c比较，如果a<c，那么让a和c的值再交换，从而保证a是三个数中的最大数；假设b中存放的是第二大的数，c中存放的是第三大的数，怎么实现呢？如果b<c，那么让b和c的值进行交换，保证b>=c，最后输出a，b，c即可。

程序如下：

                            #include<iostream>
                            using namespace std;
                            int main() {
                                float a, b, c, temp;
                                cin>>a>>b>>c;
                                if (a < b) { //交换a和b的值
                                  temp = a;
                                  a = b;
                                  b = temp;
                                }
                                if (a < c) { //交换a和c的值
                                  temp = a;
                                  a = c;
                                  c = temp;
                                }
                                if (b < c) { //交换b和c的值
                                  temp = b;
                                  b = c;
                                  c = temp;
                                }
                                cout<<a<<","<<b<<","<<c;
                                return 0;
                            }

说明？： 方法一和方法二哪种方法更好，为什么？，从上面的问题我们可以看出，同一个问题的解决办法可能是多种多样的，也就是我们所说的算法不一样，不同的算法解决问题的局限性，程序表达的便捷性以及我们后续着重关注的效率都是不一样的，一个问题的解决从算法设计的角度来看没有标准答案，只有更好的答案，这也是算法设计的魅力所在。

3.3.3分支结构程序设计实例

【例3.19】 在劳动技术课上，老师拿来了不同长度的铁丝，给每个同学发一根铁丝，要求用手上的铁丝制作固定面积的矩形框，小明想利用计算机帮助大家求出矩形的长和宽，这样能够快速完成任务，当然解决问题的算法是大家共同完成的。

输入样例：
18 20
输出样例：
矩形的长和宽分别为5，4
输入样例：
8 5
输出样例：
找不到这样的矩形

分析： 设铁丝的长度为l，面积为s，这是已知的，设所求矩形的长度为x，则宽度为l/2-x。那么有：
x(l/2-x)=s
化简后得：
x²-lx/2+s=0
因此问题就转化为了我们数学上熟知的求解一元二次方程的解。
根据解一元二次方程根的步骤，我们可以得到解决该问题的算法步骤如下：
（1）输入铁丝的长度l和面积s；
（2）输入铁丝的长度l和面积s；
（3）计算一元二次方程判别式：d=l*l/4-4*s；
（4）如果d<0,则输出没有这样的矩形；
（5）否则，如果d=0,则求解xl=2x=l/4,输出解，如果d>0，求解x1=(l/2+sqr(d))/2,x2=x1=(l/2-sqr(d))/2，输出解；

程序如下：

                            #include<iostream>
                            #include<cmath>
                            using namespace std;
                            int main() {
                                double l, s, x1, x2;
                                double d;
                                cin>>l>>s;
                                d = l * l / 4 - 4 * s;
                                if (d < 0) {
                                    cout<<"找不到这样的矩形"<<endl;
                                } else {
                                    if (d == 0) {
                                        x1 = x2 = 1 / 4;
                                    } else {
                                        x1 = (l / 2 + sqrt(d)) / 2;
                                        x2 = (l / 2 - sqrt(d)) / 2;
                                }
                                cout<<"矩形的长和宽分别为："<<x1<<","<<x2<<endl;
                                }
                                return 0;
                            }

说明： 本题把一个实际问题用数学的一元二次方程求解，提供了一种把朴素的数学分析转化为用数学方程表示的方法。

【例3.20】 在大学校园里由于校区很大，没有自行车上课办事都很不方便，但实际上，并非去办任何事情都是骑车快，因为骑车时总需要找车、开锁、停车、锁车等繁琐的过程都会耽误一些时间，假设找到自行车、开锁并骑上自行车的时间为27秒，停车锁车的时间为23秒，步行每秒行走1.2米，骑车每秒行走3.0米，输入距离（单位：米）输出骑车快还是走路快。分别用walk、same 、bike表示走路快，一样快和自称车快。

输入样例：
90
输出样例：
walk
输入样例：
100
输出样例：
same

分析：设距离为dis，则骑车时间为：t1=dis/3+27+30，走路时间为t2=dis/1.2,如果t1>t2,则输出walk，如果t1==t2则输出same，否则输出bike。

程序如1下：

                            #include<iostream>
                            using namespace std;
                            int main() {
                                double dis;
                                double t1, t2;
                                cin>>dis;
                                t1 = dis / 3 + 27 + 23;
                                t2 = dis / 1.2;
                                if (t1 > t2)
                                cout<<"walk"<<endl;
                                else if (t1 == t2)
                                cout<<"same"<<endl;
                                else
                                cout<<"bike"<<endl;
                                return 0;
                            }

说明： 在测试数据中，当距离为100时，计算记过t1=250/3，t2=250/3,应该输出的是“same”，然而程序运行结果却是“bike”，为什么呢？因为程序中第7行dis/3和第8行dis/1.2时由于除不尽，浮点数的运算会存在误差，导致计算出的t1不等于t2，如何解决呢？对于实数运行的结果要特别注意误差问题，关于误差问题，根据实际情况可以有不同的解决方案，对于本问题，将t1和t2都乘以6再进行比较，t1=dis*2+(27+23)*6,t2=dis*5把问题转化为乘法运算，因此消除因为除不尽而带来的误差。

程序如2下：

                            #include<iostream>
                                using namespace std;
                                int main() {
                                  double dis;
                                  double t1, t2;
                                  cin>>dis;
                                  t1 = dis * 2 + (27 + 23) * 6;
                                  t2 = dis * 5;
                                  if (t1 > t2)
                                    cout<<"walk"<<endl;
                                  else if (t1 == t2)
                                    cout<<"same"<<endl;
                                  else
                                    cout<<"bike"<<endl;
                                  return 0;
                            }

【例3.21】 小明知道“先有鸡还是先有蛋”的答案，他和n个人说了答案，不过他对其中的x个人故意说了错误的答案，然后有一个人问了这n个人问题的答案，有m个人说先有蛋，有n-m个人说先有鸡，已知其中有y个人故意说了小明告诉他们的相反的答案，现在给出n、m、x、y的值，问能否推测出答案，或者多解，或者无解。如果答案是鸡，输出“chicken",如果答案是蛋输出“egg",如果两个条件都满足，则输出"ambiguous"，如果都不满足，输出“this is a lie"。

输入样例：
10 10 0 0
输出样例：
egg
输入样例：
60 40 0 30
输出样例：
this is a lie
输入样例：
60 20 2 25
输出样例：
chicken
输入样例：
20 10 5 5
输出样例：
ambiguous

分析： 根据题意，对于给定的数据n,m，x，y，我们需要推测出是先有鸡还是先有蛋、多解或无解，从已知数据推测出答案有一定的难度。我们可以试着反过来分析，因为答案只有4种，不妨先假设是是其中的一个答案，然后根据已知数据判断该答案是否正确。这种解决问题的方法称为判定性问题求解法。
假设答案是先有鸡，根据数据推理如下：
(1)根据题意，n个人中，n-x个人被告知是先有鸡，x人被告知是先有蛋
(2)这n个人说出答案的过程，有y个人说出的答案与其被告知的相反，假设鸡说成蛋的有a人，蛋说成鸡的有b人，那么有：a+b=y(一式)。
(3)说出蛋的人数m=被告知是蛋的人数x+被告知是鸡的人数中“叛变”的人数a-被告知是蛋的人中“叛变“的人数b，即：m=x-b+a（二式）。
(4)联立一式和二式可得：a=(y+m-x)/2,b=(y-m+x)/2。
（5）若a，b都为正整数（若a为整数，b也一定为整数），且0<=a<=n-x、0<=b<=x，则说明“先有鸡“的假设是成立的
（6）上述的条件表达式为：(y+m-x)%2==0&&n-x>=(y+m-x)/2&&(y+m-x)/2>=0&&x>=(y-m+x)/2&&(y-m+x)/2>=0
（7）同理要证明答案是先有鸡的假设是否正确的条件为：0<=(y+n-m-x)/2&&(y+n-m-x)/2<=n-x&&(m+x+y-n)/2>=0&&(m+x+y-n)/2<=x&&(m+x+y-n)%2==0

程序如1下：

                             #include<iostream>
                             using namespace std;
                             int main() {
                                   int x, y, m, n;
                                   bool chicken, egg;
                                   cin>>n>>m>>x>>y;
                                   chicken = 0;
                                   egg = 0;
                                   if ((y + m - x) % 2 == 0 && n - x >= (y + m - x) / 2 && (y + m - x) / 2 >= 0 && x >= (y - m + x) / 2 && (y - m + x) / 2 >= 0)
                                     chicken = 1;
                                   if (0 <= (y + n - m - x) / 2 && (y + n - m - x) / 2 <= n - x && (m + x + y - n) / 2 >= 0 && (m + x + y - n) / 2 <= x && (m + x + y - n) % 2 == 0)
                                     egg = 1;
                                   if (chicken == 0 && egg == 0)
                                     cout<<"this is a lie"<<endl;
                                   if (chicken == 0 && egg == 1)
                                     cout<<"egg"<<endl;
                                   if (chicken == 1 && egg == 0)
                                     cout<<"chicken"<<endl;
                                   if (chicken == 1 && egg == 1)
                                     cout<<"Ambiguous"<<endl;
                                   return 0;
                             }

练习题

(1) 某市的IC卡电话计费标准如下：首次0.5元/3分钟（不足3分钟按3分钟计算），之后是0.2元/1分钟，已知某人打一次电话话费了x元，请问这个人打了多长时间的电话？（精确到分钟）。
(2) 输入一个不多于四位的正整数，求出它是几位数，并分别打印出各位上的数字。