4.2while循环
【例4.8】
考试结束后,老师想计算全班同学的平均分,你能帮助老师吗?现在无法知道参考人数,但是能够确定参加考试的同学的成绩都不是0分。
- 分析: 计算平均分,需要计算出总分和总人数,所以本问题转化为先计算总分和总人数,我们用变量tot存放总分,用pep来存放人数。现在要做的就是:每读入一个非0的成绩,就将其加入tot 并且将总人数tot加1.这个读成绩、累加、计数的过程一直重复到读入的成绩为0为止,我们得到若干个考试成绩,以“0”作为成绩读入结束的标志。
程序如下:
#include<iostream>
using namespace std;
int main() {
float score, tot = 0;
int pep = 0;
cin>>score;
while (score != 0) {
pep++;
tot = tot + score;
cin>>score;
}
cout<<tot/pep<<endl;
return 0;
}
- 说明: 程序中使用while循环语句完成了重复操作的任务。while循环语句的使用规则是怎么样的?whie是如何实现重复操作的呢?while循环与for循环有什么区别和联系呢?
- 带着这些问题,本节我们将学习C++语言的whie循环语句。
4.2.1while循环语句的格式与功能
格式:
- 格式1:
- while(表达式)
- 语句;
- 格式2:
- while(表达式)
- {
- 语句1;
- 语句2;
- 语句……;
- }
- 跟for循环语句一样无论是格式1中的“语句”还是格式2中的“{语句1;语句2;……}”,都是while循环语句中需要重复执行的内容,即while循环语句的循环体。
功能:
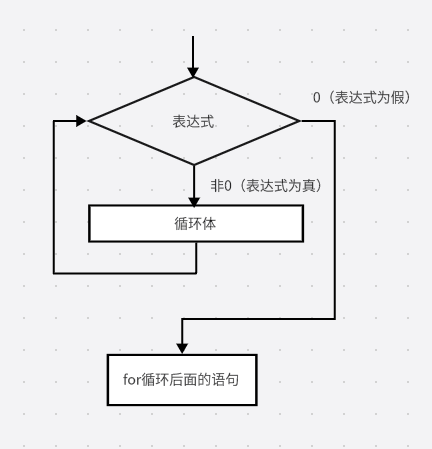
- 当表达式的值非0(表达式为真)时,不断地执行循环体中的语句,当表达式的值为0(表达式为假)时结束while循环。因此用while循环语句实现的循环被称为“当型循环”
- while循环的执行流程如下所示:
-
【例4.9】
写出下列程序的运行结果。
程序如下:
#include<iostream>
using namespace std;
int main() {
int i = 1;
while (i <= 5) {
cout<<i;
i++;
}
return 0;
}
- 说明: 只有表达式的值非0,循环体才会被执行,首次执行while的表达式也不例外(若表达式最初的值为0,则根本不执行循环体)。
- 根据上述说明,程序的第4行对i进行初始化为1,判断第5行的条件i<=5,表达式成立,则执行循环体:输出i的值,i的值自增1,再判断表达式是否还成立……
- 我们可以用下表来模拟程序的执行过程:
-
i的取值 表达式i<=5的结果 循环体的执行情况 1 非0 输出1,i更新为2 2 非0 输出2,i更新为3 3 非0 输出3,i更新为4 4 非0 输出4,i更新为5 5 非0 输出5,i更新为6 6 0 退出循环 - 对比本例与上一节中用for循环语句输出1~5之间所有整数的程序,二者在功能上是一致的,但是语句表示上有所不同。你能说出用while循环替换for循环的一般规律吗?
- 如果我们将程序中的第4行i的初始化变为i=6;程序的运行结果会有什么样的变化。
【例4.10】
写出下面程序的运行结果。
程序如下:
#include<iostream>
using namespace std;
int main() {
int i = 1;
while (i <= 5) {
cout<<i;
}
return 0;
}
- 说明: 为了使循环能够终止,while循环体中一定要有影响表达式值的操作,否则该循环就是一个死循环。
- 程序第5行使用逗号分隔的语句序列,同时对两个循环控制变量进行初始化,i的初始化值为0,j的初始化值为10,在增量部分,i每次的增量为增1,j每次的增量为减1。
- 相对于上例,本程序的循环体中少了“i++"这条语句,i的值就始终不会改变,所以while表达式的值就始终为非0,程序就一直输出i的值1,进入死循环
- 我们可以用下表来描述程序的执行过程:
-
i的取值 表达式i<=5的结果 循环体的执行情况 1 非0 输出1 1 非0 输出1 1 非0 输出1 1 非0 输出1 1 非0 输出1 …… …… ……
4.2.2while循环语句的应用
- 【例4.11】 在银行取款时,我们需要输入密码(由6位数字组成)。密码正确才可以进行取款操作:若连续三次输入密码错误,就会冻结账号。现在请你编写一个程序,模拟验证密码的过程。
- 输入格式:
- 每次输入6为数字
- 输出格式:
- 给出提示信息:正确、错误、冻结
- 分析: 对于用户来说,做的就是反复输入6位数字密码的操作。每出入一次密码可能有三种情况:。
- (1)输入错误,但输入次数不超过3次,输出“错误”
- (2)输入错误,输入错误次数超过3次,输出“冻结”
- (3)输入未超过三次,密码正确,输出“正确”,退出循环
- 综上,我们可以设置循环的条件为:输入次数不超过三次且输入不正确。
方法一程序如下:
#include<iostream>
using namespace std;
int main() {
int mima = 111000;
int x = 0, n = 0;
while (n < 3 && x != mima) {
n++;
cin>>x;
if (x != mima)
cout<<"错误"<<endl;
}
if (x == mima) cout<<"正确"<<endl;
else if (n == 3) cout<<"冻结"<<endl;
return 0;
}
思考:
如果将程序中的第12行和第13行写成if (n == 3) cout<<"冻结"<<endl;和elif (x == mima) cout<<"正确"<<endl;,可不可以,为什么?
【例4.12】
判定给定的正整数n是否为质数,是,输出Yes,否则,输出No。
- 分析: 根据数学知识,质数是这样的约定:除了1和它本身不再具有其他约数的数,就是质数。
- 根据约定,我们可以这样想:要判断n是不是质数,我们把2~n-1的整数挨个拿出来赋给i这个变量,然后用i去除n,如果在这个范围内我们找到一个数i能够整除n,那么就说明 除了1和n本身,n还有其他的约数,因此n就不是一个质数,如果我们从2~n始终没有找到一个能整除n的数,那说明n只有1和它本身两个约数,因此n是一个质数。
程序如下:
#include<iostream>
using namespace std;
int main() {
int n, i;
cin>>n;
i = 2;
while (n%i!=0 && i<n)
i++;
if (i > n-1)
cout<<"Yes"<<endl;
else
cout<<"No"<<endl;
return 0;
}
- 思考:
- (1)上述程序能解决大多数质数的判定。从严谨的角度考虑,程序中应该加上哪些处理,才能正确判断任意正整数是否为质数?
- (2)程序中,除数的上界我们限定为n-1,这个数字能否缩小?这个数字可以怎么优化?
【例4.13】
输入一个正整数,输出其位数。
- 分析: 当输入的正整数不是一位数时,我们要用累计的方法完成位数统计:设定计数器num,取出正整数的个位数字,初始化为1,从正整数中去除掉个位数字,对去除个位数字的正整数再取出 个位数字,num再加1,……直到这个数变为0为止。我们不难发现这就是一个循环的过程。
程序如1下:
#include<iostream>
using namespace std;
int main() {
int n, num = 0;
cin>>n;
while (n != 0) {
n /= 10;
num++;
}
cout<<num<<endl;
return 0;
}
- 思考:
- 如果我们将程序修改为“输入一个正整数,并计算该正整数各个位上的数字之和是多少?”程序应该怎么改?。
【例4.14】
输入任意两个自然数,求他们的最大公约数。
- 方法一分析: 求任意两个数a和b的最大公约数,可以想到公约数最大的可能就是a和b两个数中的较小者min,最小的可能是1.所以设最大公约数gcd从min开始进行判断,若gcd>1并且没有同时被a 和b整除,就将gcd减1,重复判断是否整除。
程序如下:
#include<iostream>
using namespace std;
int main() {
int a, b, gcd;
cin>>a>>b;
gcd = a > b ? b : a;
while (gcd > 1 && (a%gcd != 0 || b%gcd != 0))
gcd--;
cout<<gcd<<endl;
return 0;
}
- 方法二分析: 这里我们来学习一个数学技巧——辗转相除法:辗转相除法也叫欧几里得算法,对任意两个自然数a和b,如果q和r是a除以b的商和余数,那么a和b的最大公约数等于b和r的最大公约数。
- 具体的求解过程描述如下;
- (1)a÷b=q……r1
- (2)若r1=0,则a和b的最大公约数就是b。
- (3)若r1!=0,则继续做除法取余运算b÷r1=q……r2。
- (4)若r2=0,则r1和r2的最大公约数就是r2。
- (5)若r1!=0,则继续做除法取余运算r1÷r2=q……r3。
- (6)如此重复下去,直到出现整除为止,余数为0时的除数就是a和b的最大公约数。
程序如下:
#include<iostream>
using namespace std;
int main() {
int a, b, r;
cin>>a>>b;
r = a % b;
while (r != 0) {
a = b;
b = r;
r = a % b;
}
cout<<b<<endl;
return 0;
}
- 说明:
- 在使用循环解决实际问题是,具体使用哪一种语句并没有硬性规定,往往跟我们个人习惯和要解决的问题有关。
4.3do——while循环
【例4.15】
对于给定的自然数n求使得1+2+3+4+5+……+i>=n成立的最小i的值。
- 分析: 这个题目的实质是对一个有规律的数值序列求和,但是数值序列的个数不能直接确定。我们需要根据序列的和判断循环是否结束。因此我们能做的就是不断的累加直到序列之和大于等于n为止。
程序如下:
#include<iostream>
using namespace std;
int main() {
int n, i = 1, sum = 0;
cin>>n;
do {
sum += i;
i++;
} while (sum < n);
cout<<i-1<<endl;
return 0;
}
- 说明: 累加求和的过程至少要做一次加法。程序中使用do——while语句解决这个重复操作的过程。
- do——while循环语句是C++中永远忽解决至少执行一次重复操作的循环语句。那么如何使用do——while语句解决重复操作的问题呢?什么样的重复操作问题比较适合选择do——while语句呢?本节,我们将学些C++中的do——while语句。
4.3.1do-while循环语句的格式与功能
格式:
- 格式1:
- do
- 语句;
- while(表达式);
- 格式2:
- do
- {
- 语句1;
- 语句2;
- 语句……;
- }
- while(表达式);
- 跟for循环语句和while循环语句一样无论是格式1中的“语句”还是格式2中的“{语句1;语句2;……}”,都是do——while循环语句中需要重复执行的内容,即do——while循环语句的循环体。
功能:
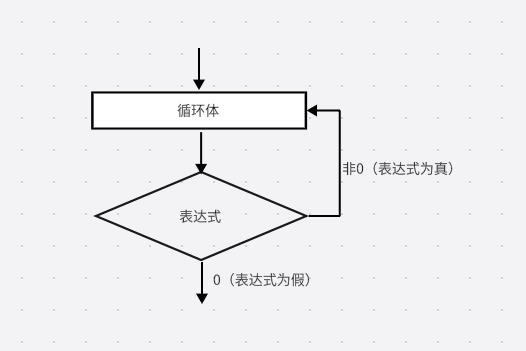
- 重复执行循环体,直到表达式的值为假(0),因此用while循环语句实现的循环被称为“当型循环”,与while循环相比,do——while循环时先执行循环体,后判断表达式的真假。
- do——while循环的执行流程如下所示:
-
【例4.16】
写出下列程序的运行结果。
程序如下:
#include<iostream>
using namespace std;
int main() {
int i = 1;
do {
cout<<i;
i++;
} while (i < 1);
return 0;
}
- 说明: do-while循环语句是在执行循环体语句之后才去判断表达式的真假,所以do-while循环最少都要执行一次循环体。
- while循环语句在进入循环之前就检查条件表达式的值,于是肯能造成while循环的循环体一次也不执行。
【例4.17】
写出下面程序的运行结果。
程序1如下:
#include<iostream>
using namespace std;
int main() {
int i = 1;
do {
cout<<i;
i++;
} while (i <= 5);
return 0;
}
程序2如下:
#include<iostream>
using namespace std;
int main() {
int i = 1;
do {
i++;
cout<<i;
} while (i <= 5);
return 0;
}
- 说明: 在do-while语句的条件一样的情况下,循环体中语句的顺序不一样,执行的结果也能也会不一样。
- 在上面的两个程序中都用了do-while循环语句来控制循环,但是循环体部分语句的顺序不一样,(第6行和第7行),程序1中当输出i的值为5之后,i的值右自增了1变成了6, 再去判断表达式不成立,退出循环,程序2中输出5之后,去判断表示式仍然是成立的,这时还要再去执行循环体,i的值右自增1变成6,并进行输出,此时再去判断表示才不成立, 循环才结束。
- 我们可以用下表来描述两个程序的执行过程:
-
i的取值 程序1中循环体的执行情况 程序2中循环体的执行情况 1 输出1,i更新为2 i更新为2,输出2 2 输出2,i更新为3 i更新为3,输出3 3 输出3,i更新为4 i更新为4,输出4 4 输出4,i更新为5 i更新为5,输出5 5 输出5,i更新为6 i更新为6,输出6 6 退出循环 退出循环
【例4.18】
写出下列程序的运行结果。
程序如下:
#include<iostream>
using namespace std;
int main() {
int i = 1;
do
cout<<i;
while (i < 5);
return 0;
}
- 说明: 一样的,为了使do-while循环能终止,循环体中一定要有影响表达式值的操作,否则该循环就会陷入死循环。
- 在这个程序中,循环体中没有改变i值的语句,i的值始终保持进入do-while循环之前获得的值1,而表达式是i<=5。表达式的值始终为1(非0),循环体将进入死循环。
4.3.2do-while循环语句的应用
【例4.19】
针对计算机随机产生的两个三位数,用户计算并输入其和,直到计算正确,输出所用的计算次数。
- 分析: 根据题意,输入的数字不正确,就要重新计算并输入。这时很明显的循环思想,而输入的数字不正确就是循环的条件。
- 因为至少要输入一次并判断计算是否正确,符号do-while循环至少执行一次循环体的特征。
程序如下:
#include<iostream>
#include<cstdlib>
#include<ctime>
using namespace std;
int main() {
int x, y, n, num = 0;
srand(time(NULL)); // 随机数种子函数
x = 100 + rand() % (999 - 100 + 1); // 随机产生一个三位数
y = 100 + rand() % (999 - 100 + 1); // 随机产生一个三位数
do {
cout << x << "+" << y << "=?";
cin >> n;
num++;
} while (n != x + y);
cout << num << endl;
return 0;
}
- 说明:
- (1)srand()是一个随机种子函数
【例4.20】
计算与任意输入的十进制正整数等值的二进制数共有几位数字?
- 分析: 二进制数中只有0和1两个数码,也就是说它的每位数位上是有两种可能,非0即1.二进制的基数为两个。进位规则是“逢二进一”,借位规则是“借一当二”。
- 将一个十进制数转化为2进制数通常采用“除二取余,倒序连接的方法”,将十进制的13转化为2进制的过程如下图所示:
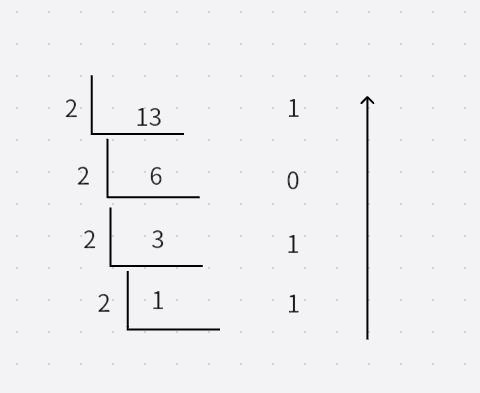
- (13)10=(1101)2
- 反之,将二进制转化为十进制,采用“权值展开法”,例如:
- (1101)2=(1*20+0*21+1*22+1*23)10=(8+4+0+1)10=(13) 10
- 要解决本题,可以借助十进制转化为二进制的思想,每一次除法产生一个二进制位,我们就可以进行一次位数统计。根据上图的方法,转化的过程本质就是在商是非0的条件下,反复除以2的操作
程序如下:
#include<iostream>
using namespace std;
int main() {
int n, num = 0;
cin >> n;
do {
num++;
n /= 2;
} while (n != 0);
cout << num;
return 0;
}
- 思考:
- 在程序上做响应的修改,实现将一个十进制数转化为二进制数并进行输出。
练习题
- (1) 圆周率的近似值可以用公式:PI/4=1-1/3+1/5-1/7+1/9……请你计算当某项绝对值小于10-6时,PI的近似值是多少
- (2) 一小球从200m高处自由落下,每次落地后返回原高度的一半,然后再落下,再弹起,……一直到小球弹起的高度不足0.5m时,计算小球一共经历了多少路程?。
- (3) 给定一个整数,请将该数各个数位上的数字反转得到一个新数。新数也满足整数的常见形式,即除非给定的原数为0,否则反转后得到的新数的最高位数字不能为0。
- 输入n+1行,第一行为A国参与决赛项目的天数,其后n行,每一行是该国某一天获取金、银、铜牌的数量,以一个空格分隔。
- 输出仅一行,包含四个整数,分别为A国获取的金、银、铜牌以及总的奖牌数量。一个空格分隔。
- 输入样例1:
- 123
- 输出样例1:
- 321
- 输入样例2:
- -380
- 输出样例2:
- -83
- (4) 现代数学的注明证明之一是Georg Cantor证明了有理数是可枚举的。他是用下面的方式来证明这一命题的:
- 1/1 1/2 1/3 1/4 1/5……
- 2/1 2/2 2/3 2/4……
- 3/1 3/2 3/3……
- 4/1 4/2……
- 5/1 ……
- 我们以z字型给上表的每一项编号:第一项是1/1,后面是1/2,2/1,3/1,2/2……输入正整数n,输出表中的第n项。
- 输入样例:
- 7
- 输出样例:
- 1/4