程序段的反复执行【循环】
- 我们在学习和生活中常常会需要做一些重复性的工作,例如我们要把书包里的10本书摆放在书架的制定位置上,要做的工作就是重复十次:拿起书——找位置——摆好书,如果用程序的方式描述这项工作。 那就是10个重复的程序段,可是我们真的要写出10段相同的程序段吗?如果是,假如我们要放的书是100本,1000本,那我们的程序段是不是就要写100个1000个重复的程序段了?
- 事实上,反复执行同样的操作,这就是循环的思想。在c++语言中,提供了for循环,while循环和do—while循环三种不同形式的循环语句。
4.1for循环
【例4.1】
对于任意给定的正整数n,输出1~n的平方数
- 分析:对于任意正整数i,其对应的平方数就是i*i。解决本题就要做n次重复操作:i的取值范围从1变化到n,对于i的每一个1取值,输出其平方数。
程序如下:
#include<iostream>
using namespace std;
int main() {
int i, n;
cin>>n;
for (i = 1; i <= n; i++) //重复操作
cout<<i * i<<" "; //输出i的平方
return 0;
}
- 说明: 程序中第6行使用了for(i=1;i<=n;i++)语句,控制第7行的cout<<i * i<<" ";语句执行n次,避免了重复书写n段cout<<i * i<<" "语句的问题。
- 那么,for语句的使用规则是什么,什么样的重复操作适合使用for语句?for语句又是如何解决重复操作的呢?本节我们将学习C++中的for语句。
4.1.1for语句的格式与功能
格式:
- 格式1:
- for(循环控制变量初始化;循环控制条件;循环控制变量增量)
- 语句;
- 格式2:
- for(循环控制变量初始化;循环控制条件;循环控制变量增量)
- {
- 语句1;
- 语句2;
- 语句……;
- }
- 无论是格式1中的“语句”还是格式2中的“{语句1;语句2;……}”,都是for语句中需要重复执行的内容,即for语句的循环体。
功能:
- 对于使循环控制条件成立的每一个循环控制变量的取值,都要执行一次循环体。for循环的执行流程如下图所示:
-
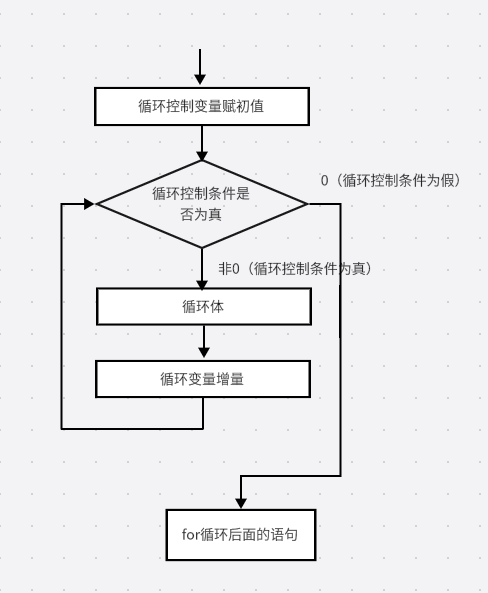
【例4.2】
写出下列程序的运行结果。
程序如下:
#include<iostream>
using namespace std;
int main() {
int i;
for (i = 1; i <= 5; i++) {
cout<<i;
}
return 0;
}
- 说明: 循环控制变量初始化的作用是让循环控制变量获得一个初值;循环控制条件通常用来控制循环控制变量的范围,当循环控制变量的值让循环控制条件的值为假(即循环控制条件不成立) 的时候,这个循环就会终止;而循环控制变量增量则是改变循环控制变量的值的语句。
- 程序第5行中的“i=1"是给循环控制变量i赋一个初值;“i<=5”约束了循环控制变量i的1取值范围不能超过5;“i++”(与i=i+1是等价的)决定了循环控制变量i的增量是每次递增1。
- 因此程序运行时,循环控制变量i的取值以及循环体的执行情况如下表所示:
-
i的取值 循环体的执行情况 1 输出1 2 输出2 3 输出3 4 输出4 5 输出5 6 退出循环
【例4.3】
写出下面程序的运行结果。
程序如下:
#include<iostream>
using namespace std;
int main() {
int i, j;
for (i = 0, j = 10; i < j; i++, j--)
cout<<i<<" "<<j<<endl;
return 0;
}
- 说明: 在循环控制变量的初始化部分和增量部分,可以用逗号分隔的语句序列,来同时进行多个动作。
- 程序第5行使用逗号分隔的语句序列,同时对两个循环控制变量进行初始化,i的初始化值为0,j的初始化值为10,在增量部分,i每次的增量为增1,j每次的增量为减1。
- 因此程序运行时,循环控制变量i和j的取值以及循环体的执行情况如下表所示:
-
i的取值 j的取值 循环体的执行情况 0 10 输出0 10 1 9 输出1 9 2 8 输出2 8 3 7 输出3 7 4 6 输出4 6 5 5 退出循环
【例4.4】
写出下面程序的运行结果。
程序如下:
#include<iostream>
using namespace std;
int main() {
int i, sum;
sum = 0;
for (; i <= 100;) {
sum += i;
i++;
}
cout<<i<<" "<<sum<<endl;
return 0;
}
- 说明: for循环语句中的循环控制变量初始化、循环控制条件和循环控制变量增量可以部分或者全部省略,但是两个分号不能省。
- 在程序第6行的for语句中,省略了循环控制变量的初始化和循环控制变量增量部分,根据程序的整体逻辑,我们可以推断出该程序的功能是想要求前100个自然数的和。
- 在使用for循环时我们需要注意养成对循环控制变量赋初值的习惯。否则c++编译器会随机给循环控制变量一个初值。例如本程序在不同的环境下运行就会产生不同的结果。
4.1.2for循环语句的应用
- 【例4.5】 输出100以内的所有偶数。
- 方法一分析: 从题目看,很明显是要重复输出100以内的50个偶数。循环控制变量的初值,终止值和增量都很清楚,所以适合用for循环语句来解决问题。
- 我们可以想到对于1~100之间的100个数字i,直接重复进行判断i是否是偶数,是则输出i的值。
方法一程序如下:
#include<iostream>
using namespace std;
int main() {
int i;
for (int i = 1; i <= 100; i++)
if (i % 2 == 0)
cout<<i<<endl;
return 0;
}
说明:
程序中将1~100之间所有的整数一一列举出来,然后逐个判断是否是偶数,符合偶数的条件就输出。这种思想本质就是穷举。穷举法保证在求解问题的过程中,所有可能都会被列举到
,不会丢解。当然穷举的缺点就是有时候效率会比较低,关于穷举法,我们还会在后面的学习中进行深入了解。
- 方法二分析: 在方法一分析的基础上,再进一步分析:我们都知道,相邻偶数之间的差值为2,所以,所以我们还可以找到1~100之间的第一个偶数2初始化为循环控制变量的初始化值,以后每循环一次 循环控制变量的值就加2(循环控制变量的增量)。
方法二程序如下:
#include<iostream>
using namespace std;
int main() {
int i;
for (int i = 2; i <= 100; i += 2) {
cout<<i<<endl;
}
return 0;
}
思考:
方法一和方法二哪个方法的效率更高,为什么?。
【例4.6】
已知n个人的身高值,求出其中的最大值
- 分析: 我们联想一下上体育课时找排头的方法:先假设一个最高者作为排头,然后随便让一个人跟排头比身高,如果这个人的身高比当前的排头还要高,那么就让这个人取代当前排头作为 新排头;后面剩下的人就是重复这个过程“和当前排头比身高,如果比当前排头还要高,就替代当前排头称为新排头。“直到所有的人都比较完,此时得到的排头一定是最高的。
- 类比这种思想,我们可以先假设max存放了身高的最大值(这里可以将初始值赋值为0),读入第1个人的身高值,若比max大,就用该升高替换max的值;继续读入第2个人的身高, 若比max大,继续用该身高替换max的值,……读入第n个人的身高,若比max大,就用第n个人的升高替换max的值,不难看出,这个过程就是一个循环的过程。
程序如1下:
#include<iostream>
using namespace std;
int main() {
int i, n;
float x, max = 0;
cin>>n;
for (i = 1; i <= n; i++) {
cin>>x;
if (x > max)
max = x;
}
cout<<max<<endl;
return 0;
}
- 思考:
- (1)如果将程序中的max初始化为第一个人的身高,可不可以?如果可以请自己编程实现
- (2)结合例题编程求出最小身高值。
【例4.7】
斐波那契数列是一个特殊的数列:数列的第一项和第二项分别为0和1,从第三项开始,每一项都是其前面两项之和。即0,、1、1、2、3、5、8、13、……请编程输出该数列的前40项。
- 分析: 根据题目描述,对于数列中的第i项(i>=3)c,可以表示为其前面两项a和b之和,即c=a+b。
- 由于题目只要求输出前40项的值,我们就不必将40项的值全部保存下来,只需要边计算边输出即可:
- (1)对于a、b分别初始化为0、1,并输出它们的值;
- (2)计算第三项c=a+b;
- (3)计算第四项。此时它的前面两项分别为当前的b和c,而当前a的值不需要被保存。为保持描述的连贯性,我们在输出第三项后可以做以下更新:
- a=b;
- b=c;
- 这样我们在求第四项的值时,又可以表示为c=a+b,输出c便又输出了第四项。
- (4)求解其后各项的值,都可以用类似(3)的方法,先更新a和b的值,计算c=a+b,然后输出即可。
- 分析至此,我们可以发现:解决本题,从第三项开始便用到了重复操作:c=a+b并输出c,更新a和b的值。
程序如1下:
#include<iostream>
using namespace std;
int main() {
int i, a = 0, b = 1, c;
cout<<a<<endl;
cout<<b<<endl;
for (i = 3; i <= 40; i++) {
c = a + b;
cout<<c<<endl;
a = b;
b = c;
}
return 0;
}
- 说明:
- 程序中,用了重复更新a、b值的方法来求得数列每一项的值。这种思想,本质就是一中迭代,关于迭代,我们后面会深入研究。
练习题
- (1) 班上有学生若干名,给出每名学生的年龄(整数),求班上所有学生的平均年龄,保留到小数点后两位。
- 输入包含若干行,第一行有一个整数n(1<=n<=100),表示学生的人数,其后n行每行一个整数,表示每个学生的年龄,取值为15到25。
- 输入样例:
- 2
- 18
- 17
- 输出样例:
- 17.50
- (2) 给定一个长度为n的非负整数序列,请计算出序列的最大跨度值(最大跨度值=最大值-最小值)。
- 输入一共两行第一行为序列的个数n(1<=n<=100)第二行为n个不超过1000的非负整数,整数之间以一个空格分隔。
- 输入样例:
- 6
- 3 0 8 7 5 9
- 输出样例:
- 9
- (3) 2008年北京奥运会,A国的运动员参加了n(1<=n<=100)天的决赛项目,现在要统计A国所获得的金、银、铜牌数据以及总奖牌数。
- 输入n+1行,第一行为A国参与决赛项目的天数,其后n行,每一行是该国某一天获取金、银、铜牌的数量,以一个空格分隔。
- 输出仅一行,包含四个整数,分别为A国获取的金、银、铜牌以及总的奖牌数量。一个空格分隔。
- 输入样例:
- 3
- 1 0 3
- 3 1 0
- 0 3 0
- 输出样例:
- 4 4 3 11